Histoire du dé
Selon la légende grecque, le héros Palamède inventa les dés pour distraire ses compagnons qui, dix années durant, firent le siège de Troie. Nous savons même, d'après Homère, qu'à l'époque, les notables pratiquaient le jeu assis sur des peaux de bœuf devant la porte du palais d'Ulysse. En fait, les dés étaient connus plusieurs siècles avant la guerre de Troie. On en a retrouvé dans des tombeaux égyptiens et il est déjà fait allusion aux funestes effets du goût immodéré pour les jeux de dés dans le plus ancien des quatre livres sacrés de l'Inde.

Le dé qui doit son nom au latin datura (donné par le sort), en grande faveur chez les Grecs et les Romains, apparaît en France dès le XIIe siècle. Le jeu connaît vite un grand succès, au temps de la Chevalerie. Il existe même à Paris et dans certaines grandes villes des Académies de Jeu de dés (scholae deciorum). La corporation des déciers ou fabricants de dés devient fort importante et le demeure même après l'apparition des premiers « cartiers » à la fin du XIVe siècle. Nombre d'ordonnances royales, dont une de Saint-Louis interdisent ou réglementent, sans grand effet, les jeux de dés.
La passion du jeu gagne aussi le petit peuple. On en a pour preuves notamment une ordonnance du Magistrat de Lille de 1382 portant défense aux guetteurs de jouer aux dés et au tric-trac. En 1398, la Prévôté de Paris interdit aux « gens de métier », à peine de prison, de jouer les jours ouvrables. Plus tard, assez joueur lui-même, le bon roi Henri IV, reprenant une idée de son prédécesseur, décide de tirer « quelque commodité » des cartes et des dés, en les soumettant à l'impôt. On n'en joue pas moins et si les déciers devenus moins nombreux se montrent récalcitrants, les cartiers vont mettre tous les moyens en œuvre pour lutter contre cette façon d'aider au rétablissement des finances.
Si le dé demeure le symbole du hasard, les jeux de dés ont perdu avec le temps les graves défauts dont on les accablait. Le démon du jeu a trouvé tant de nouveaux moyens de tentation que les dés ne constituent plus guère la plupart du temps qu'une aimable récréation. En dépit des apparences pourtant le jeu n'est pas toujours aussi enfantin qu'il paraît. C'est en étudiant les chances qu'a un joueur d'obtenir un total donné en lançant deux dés, que Pascal établit les bases du calcul des probabilités. Il est bon d'y songer notamment quand on a la faculté de jouer ou non une seconde fois pour modifier un total obtenu. Dans une pensée analogue, il est souhaitable, lorsque le jeu comporte un « banquier », que chacun en tienne le rôle à son tour, pour égaliser les chances.
Quelques probabilités :
On peut jouer avec un ou plusieurs dés, qu'on place dans un cornet ou dans le creux de la main et qu'on fait rouler ensuite sur le tapis.
On « amène ›› des points (1, 2, 3, 4, 5 ou 6 points pour chaque dé), lus sur la face supérieure du dé. Quand un dé ne repose pas à plat, en raison d'un obstacle quelconque, il est dit cassé et il faut rejouer. Le point « 1 ›› est aussi nommé « As ».
Si les dés employés sont parfaitement cubiques, la probabilité d'apparition d'une face ou d'une autre est toujours la même et égale à 1/6 = 0,1666... Si l'on joue avec plusieurs dés, on peut calculer simplement la probabilité des événements envisagés, c'est-à-dire le nombre de points amenés.
Avec deux dés, il est facile de calculer le nombre total de cas également possibles. Le point 1 de la première face d'un dé, additionné aux points des six faces de l'autre, fournit six résultats : 1+1, 1+2, 1+3, 1+4, 1+5, 1+6.
Le point 2 de la deuxième face, fournit aussi six résultats : 2+1, 2 + 2, etc. Les six faces du premier dé peuvent être combinées avec les six faces du deuxième dé, il y a donc : N = 6 X 6 = 36 = 62 cas possibles.
On dit, en langage des probabilités, que ces 36 cas sont équiprobables (ils ont la même probabilité d'apparition).
Le minimum que l'on puisse tirer est 2 (1 + 1), le maximum 12 (6 + 6). A titre d'exemple, calculons la probabilité que l'on a de tirer 7 avec deux dés lancés en même temps.
On peut faire 7 de six façons différentes : 1+6, 6+1, 2+5, 5+2, 3+4, 4+3.
La probabilité de tirer 7 avec deux dés est donc de 6/36 = 0,1666...
Par contre, on ne peut faire 2 que d'une seule façon (1 + 1). La probabilité de tirer 2 avec deux dés est donc de 1/36 = 0,0277...
Avec trois dés, on obtient six fois plus de cas possibles qu'avec deux dés (chaque résultat obtenu avec deux dés peut être combiné aux six faces différentes du troisième dé). Il y a donc : N = 6 × 36 = 216 = 63 cas possibles.
De même, on aurait, avec quatre dés : N = 6 × 216 = 1296 = 64 cas possibles, et, avec cinq dés : N = 6 × 1 296 = 7 776 = 65 cas possibles.
Calculons, par exemple, la probabilité que l'on a de tirer 7 avec trois dés.
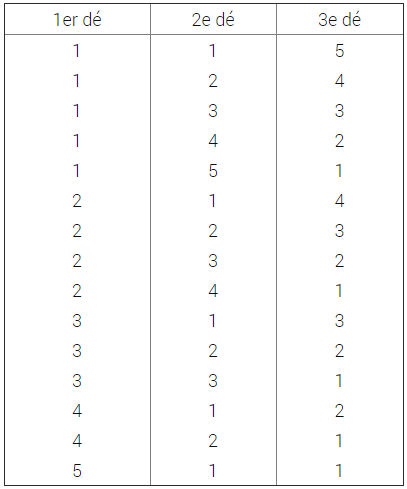
Le nombre total de cas équiprobables est 63 = 216. Le nombre de cas possibles est 15, comme il ressort du tableau ci-dessous. Donc la probabilité pour tirer 7 avec trois dés est : P = 15/216 = 0.069444… (on remarque qu'elle est inférieure à la probabilité de tirer 7 avec deux dés, probabilité qui était égale à 0,1666…).
Différentes façons de faire 7 avec trois dés :
Probabilités de tirer un nombre de points donnés avec 2, 3 ou 4 dés :
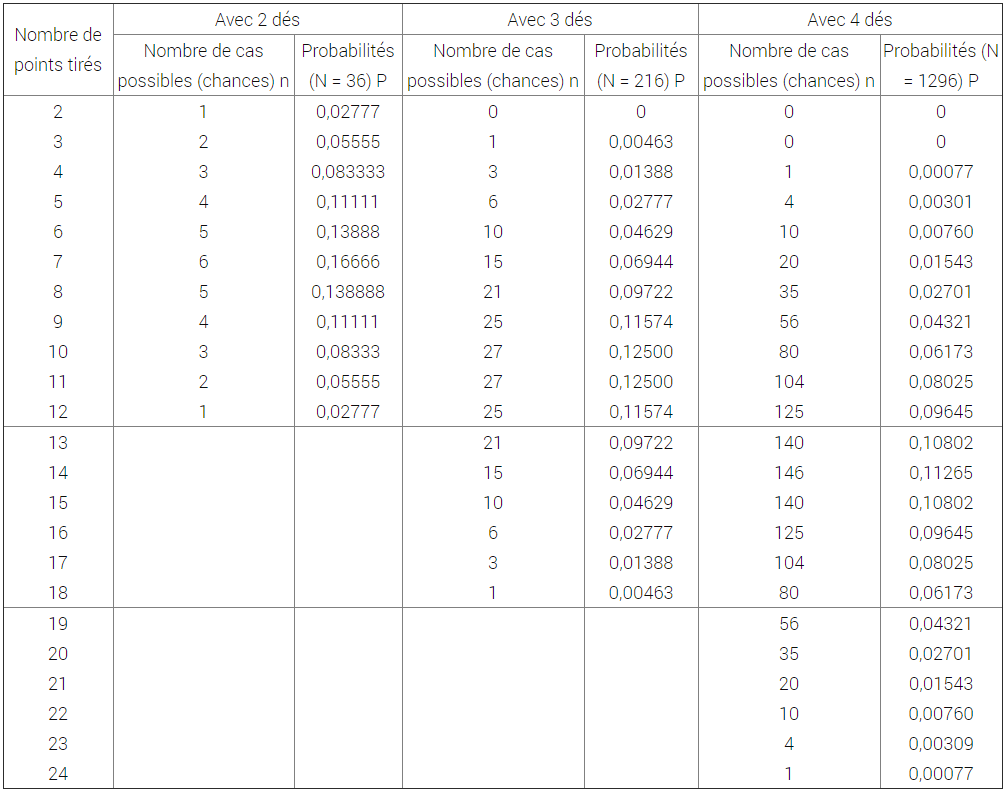
Le tableau donne le nombre de cas équiprobables de tirer un nombre de points donnés (12 au maximum avec deux dés, 18 au maximum avec trois dés, etc.) et les probabilités correspondantes (p = n/N).
Probabilité de tirer un brelan avec trois dés
un brelan est une figure composée de trois faces semblables (trois As, trois 2, etc.).
Nombre de cas total N = 216. Nombre de brelans possibles n = 6. Probabilité pour tirer un brelan : p = 6/216 = 0,02777.
Probabilité de tirer une paire (deux faces semblables) avec deux dés
N= 36, et il y a n = 6 paires possibles, donc : P = 6/36 = 0,16666.
Probabilité de tirer une paire avec trois dés
On a N = 216, et l'on peut tirer six paires avec le 1er et le 2e dé, six paires avec le 2e et le 3e dé, six paires avec le 1er et le 3e dé, soit, au total 18 paires possibles. Donc : P = 18/216 = 0,08333.
Probabilité de tirer 4-2-1 (421) avec trois dés, d'un seul coup.
Il y a N = 216 cas possibles, et l'on peut faire « 421 ›› de six façons différentes :
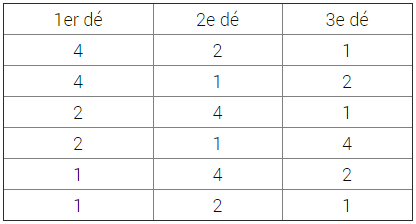
La probabilité pour faire « 421 sec » (d'un seul coup) est donc : P = 6/216 = 0,02777
On réussit ce coup un peu moins de trois fois sur cent en moyenne.
La probabilité de tirer deux fois de suite « 421 » est plus faible encore et égal à p2 = 0,02777 X 0,02777 = 0,00077.
