La mathématique des paris
La pratique des paris se confond sans doute avec l'apparition des premiers hominidés. Mais les premières tentatives de modélisation rationnelle apparaissent au 15e siècle pour des jeux interrompus. C'est la naissance du calcul des probabilités avec Pascal.
Les premières tentatives d'analyse des paris, très littéraires, sont touffues et peu claires. Elles procèdent didactiquement au moyen d'exemples numériques sans détailler la solution générale. Le problème à résoudre est pourtant simple : comment partager la somme des mises de deux ou plusieurs joueurs lorsque la partie n'est pas terminée et que l'un des adversaires possède un avantage ? Examinons le cas de deux joueurs qui misent chacun en début de partie le même montant x. Le jeu consiste en une suite d'épreuves identiques, équitables (lancement de dés non truqués par exemple), en convenant que la totalité des mises, 2x, va au premier joueur qui remportera g épreuves (g > 0). Comment partager correctement les mises si le jeu est interrompu alors que l'un des joueurs a remporté g1 épreuves et l'autre g2, avec g1 > g2 ?
Le plus ancien texte traitant du sujet est dû à Luca Pacioli, l'inventeur de la comptabilité en partie double (Summa de arithmetica, geometria, de proportioni et de proportionalita, publié à Venise en 1494). Le raisonnement de Pacioli est étrange. Il commence par calculer le nombre maximum d'épreuves possibles (2g - 1). Un résultat dont il ne se servira pas, puisqu'il se contente de répartir la somme des mises en fonction des épreuves réussies des deux joueurs : le premier reçoit 2x.g1 / (g1 + g2), et le second 2x.g2 / (g1 + g2). Pacioli s'est aussi distingué par une formule donnant le temps de doublement d'un capital placé à intérêts composés, avant l'invention des logarithmes.
Le partage équitable est déterminé par l'écart existant entre la situation des joueurs et le gain final.
Partage équitable
Cardan, dans Pratica arithmetica et mensurandi sigularis (1539), critique la méthode Pacioli en donnant plusieurs cas particuliers pour lesquels elle est absurde (absurdissimum) : le cas g2 = 0 attribue toute la mise au joueur 1 alors que ce dernier n'a pas totalement rempli le contrat. Cardan prend conscience que ce qui détermine le partage équitable est l'écart existant entre la situation des joueurs et le gain final, et non le nombre de parties gagnées. Il introduit la notion de « progression » (somme des entiers inférieurs à un nombre donné : « progressio 7 est 28 »). Cardan propose de sommer les progressions, et attribue à chaque joueur le rapport entre la progression de l'autre joueur et la somme des deux progressions. Vient ensuite le mathématicien bègue, Tartaglia, qui publie la Prima parte del Generai trattaio di numeri e misure (1556). Pour lui, le partage doit se faire en deux temps : celui qui a gagné le plus de parties peut reprendre sa mise, puis il peut revendiquer une part de la mise de son adversaire (proportionnellement au quotient de la différence de jeux remportés par le nombre g de victoires à atteindre pour être déclaré vainqueur). Le premier joueur reçoit x + x(g1 - g2) / g, et le second x(g - g1 + g2) / g. Lorenzo Forestani (mort en 1623), dans sa Pratica d'aritmetica e geometria (1603), reprend le raisonnement de Pacioli en le modifiant. Il reconsidère aussi le nombre maximum de jeux, 2g - 1. Le premier joueur a rempli une part g1 / (2g - 1) du contrat et remporte donc cette fraction de la mise totale. Le second joueur peut emporter g2 / (2g - 1) de cette mise. Quant à la fraction restante de la mise totale, (2g - g1 - g2 - 1) / (2g - 1), considérant que le jeu est équitable, il propose de la partager également entre les deux joueurs.
Les solutions proposées se réduisent à des répartitions. Avec Pascal et Fermat, un point de vue différent s'impose avec l'élaboration d'un véritable processus de décision. Reprenons les lettres de Pascal à Fermat (en 1654). Soit (g1, g2) l'état du système au moment du partage. Pour Pascal, lorsque g1 = g2 < g, les joueurs sont à égalité et chacun peut reprendre sa mise. Voyons les autres éventualités (g1 > g2). Lorsque g1 = g, le premier joueur remporte la totalité de la mise, 2x. Toutes les autres situations peuvent être déterminées de proche en proche, à partir des situations connues, par le raisonnement suivant. Partons du cas (g - 1, g - 2). Si les joueurs avaient pu jouer une partie supplémentaire, ils se seraient trouvés soit dans le cas (g, g - 2), déjà résolu, soit dans le cas (g - 1, g - 1), pour lequel on a aussi la solution. Pour Pascal, si le jeu est équitable, les deux futurs sont équiprobables (il ne le dit pas ainsi) et un calcul d'espérance mathématique s'impose (il ne l'explicite pas sous cette forme). Les joueurs recevront la moyenne des gains associés aux deux situations possibles.
Pour le premier, on a ½ . 2 x + ½ . x = 1,5 x. Le second prend ½ . 0 + ½ . x = 0,5 x. Tous les cas sont calculables de proche en proche.
L'espérance mathématique
L'idée de l'espérance mathématique est à la base du pari de Pascal. La notion d'espérance (de gain) mathématique, définie comme la somme des gains consécutifs aux différents événements envisagés, pondérée par les probabilités associées à ces gains, est avancée. Mais il existe des jeux s'accordant mal avec cette notion : une mise de départ acceptable ne peut être définie de façon raisonnable. Considérons la martingale, classique à la roulette, consistant à miser rouge ou noir, pair ou impair, manque ou passe, en négligeant la présence du 0. Ni rouge ni noir, ni pair ni impair, ni manque ni passe, il fait passer la probabilité de gagner de 1/2 à 18/37. Un joueur parie 10 € sur le rouge. S'il gagne, il double sa mise (il gagne 10 €). S'il perd, il recommence en doublant sa mise. Et ainsi de suite. Pour un nombre « infiniment grand » de tentatives, la probabilité de gain associée à cette martingale est 1/2 + 1/4 + 1/8 +... soit 1. Et l'espérance de gain du joueur est de 10 €. Mais la mise initiale à prévoir pour pouvoir jouer ainsi est infinie : 10 € + 20 € + 40 € +... Pour éviter tout problème, les casinos limitent les mises ou imposent de rejouer en cas de gain. Le paradoxe de Saint-Pétersbourg, dû à Nicolas Bernoulli (en 1713, dans une lettre à Pierre Rémond de Montmort), reprend cette martingale. On lance une pièce de monnaie. Si « face » apparait, la banque paie 2 € au joueur, et on arrête le jeu. Sinon, on relance la pièce. Si « face » apparait au second lancer, la banque paie 4 €, et on arrête le jeu. On continue ainsi : si face apparaît pour la première fois au ne lancer, la banque paie 2n € au joueur. Quelle est la mise initiale pour que le jeu soit équitable ? Daniel, cousin de Nicolas, en poste à Saint-Pétersbourg, étudie la question. Il calcule la somme des gains pondérés par les probabilités :
2 x 1/2 + 4 x 1/4 + 8 x 1/8 + ... = 1 + 1 + 1..., qui diverge. Quelle que soit la mise initiale exigée par la banque, l'espérance mathématique de gain pour le joueur est infinie ! Mais quel joueur sain d'esprit acceptera de jouer à ce jeu, surtout si la mise initiale est élevée ? Ce comportement d'apparence irrationnelle, l'aversion au risque, a été formalisé par la notion de fonction d'utilité pour donner naissance à la théorie de la décision. Le statisticien américain Bradley Efron (né en 1938) est l'auteur d'une énigme qui combine paradoxe de Condorcet et théorie des jeux.
Condorcet avait observé que des préférences individuelles ne pouvaient pas toujours être traduites au niveau collectif lorsque plus de deux candidats s'affrontent lors d'élections. Efron propose alors de choisir un dé parmi quatre (A, B, C et D). A comporte le nombre 4 sur quatre faces et 0 sur les deux autres. B contient 3 sur chaque face. C représente 2 sur quatre faces et 6 sur les deux autres. D comprend 5 sur trois faces et 1 sur les trois autres. Lorsque le joueur 1 a choisi son dé, le joueur 2 en fait autant. Puis ils s'affrontent. Comment nos deux joueurs peuvent-ils miser ? A bat B deux fois sur trois, B bat C, C bat D et D bat A deux fois sur trois. Le joueur qui commence le jeu a donc toujours une probabilité 1/3 de gagner, contre 2 /3 pour le second joueur. Les rapports de gain ne peuvent donc être égaux !
Paris sportifs : le cas des bookmakers
La législation française interdisait l'exercice des sites de paris en ligne en France en raison du monopole des paris sportifs attribué à la Française des jeux et au PMU. Ce monopole a disparu le 1 janvier 2010, conformément à la législation européenne. Un bookmaker astucieux peut tenter d'équilibrer ses activités ainsi. Soit C = {ci} l'ensemble fini des compétiteurs s'affrontant lors d'une épreuve donnée. L'ensemble fondamental des événements possibles lors du déroulement de cette épreuve est Ω = {ωi} (ωi : victoire de ci). On associe à chaque ω, une probabilité pi. Le bookmaker doit proposer un certain rapport associé aux événements élémentaires (deux contre un, trois contre un...). Le compétiteur auquel il associe la probabilité de victoire la plus élevée est le favori (s'il gagne, le rapport sera petit). Celui auquel il a associé la probabilité la plus faible est l'outsider (s'il gagne, le rapport sera élevé). Soient ki le rapport associé à la victoire de ci et xi le montant total misé sur la victoire de ci. Il existe un lien entre pi et ki. Pour être en équilibre, le bookmaker doit conserver l'inégalité suivante pour tout i :
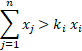
On remarque que la probabilisation n'apparaît que sous forme implicite par le biais de ki. On peut la rendre explicite en utilisant la notion d'espérance mathématique. En moyenne, notre bookmaker sera à l'équilibre si :
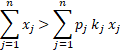
C’est-à-dire si la somme des mises lui permet de couvrir au moins l'espérance mathématique de ses débours. Cette relation doit être vraie quelles que soient les mises. On doit donc avoir pi ki < 1, quel que soit i, ce qui permet de déterminer les rapports.
Paris sportifs : le Pari mutuel urbain
Le sport hippique était répandu dans l'Antiquité. En Grèce, on prisait les courses montées, tandis qu'à Rome, le Cirque Maxime accueillait des épreuves de chars. Nul doute que ces pratiques n'aient entraîné divers paris. En Occident, l'imposition du christianisme alla de pair avec la suppression de ces épreuves. Il fallut attendre le XVIIe siècle pour voir renaître le sport hippique par la volonté de Louis XIV (1651). À partir de 1868, des paris sur les épreuves hippiques seront organisés et réglementés par le Pari mutuel hippodrome (PMH) créé sous l'impulsion de Joseph Oller (à qui on doit aussi le Moulin Rouge et l'Olympia). Son idée est de mutualiser les sommes misées et de les redistribuer aux gagnants proportionnellement au montant de leur enjeu, tout en déduisant la partie servant à financer la société organisatrice et son personnel. Ce système de pari est toujours appliqué par le PMU.
Viager et finance : le pari des banques et des assureurs
Le marché financier a vu apparaître ces vingt dernières années des produits nouveaux pour gérer et couvrir les risques liés à la possession d'actifs très volatiles. Ces produits consistent en le droit d'acheter ou de vendre une action donnée à un prix fixé à un instant déterminé : ce sont les options call (achat) ou put (vente). Il s'agit d'un pari sur la hausse ou la baisse du titre sous-jacent. Si j'ai acheté le droit d'acheter moins cher et que l'action monte, j'empoche la différence. Si j'ai acheté le droit de vendre plus cher alors que l'action a baissé, je gagne également. Dans les cas contraires, je perds ma mise. Pour valoriser ces paris, les financiers ont constaté que la notion d'espérance ne donne pas de bons résultats. Pour bien équilibrer le marché et les risques, il faut calculer une espérance mathématique dans un espace probabilisé qui n'est pas l'espace usuel (c'est l'espace neutre au risque). Voici une seule application de l'espérance à des organismes pratiquant la bancassurance : les contrats d'assurance vie (pari sur la mort ou la survie des clients). Leurs primes pures (sans frais de gestion) sont calculées au moyen de la même formule.
